|
|
|
|
Pipe Flow 3D - Pressure Drop Theory
This page describes in detail which factors need to be considered when calculating pressure drops through pipe systems, their effects on fluid flow and conditions at the pump inlet, and how Pipe Flow 3D can help with the calculations.
Resistance to fluid flow
Fluids in motion are
subjected to various resistances, which are due to friction. Friction may occur
between the fluid & the pipe work, but friction also occurs within the
fluid as sliding between adjacent layers of fluid takes place. The friction
within the fluid is due to the fluid’s viscosity.
|


[ Now superseded by
Pipe Flow Expert ]
|
When fluids have
a high viscosity, the speed of flow tends to be low, and resistance to flow
becomes almost totally dependant on the viscosity of the fluid, this condition
is known as ‘Laminar flow’.
How do you establish the
pipework resistance losses?
Before the pipework losses can be
established, the friction factor must be calculated. The friction factor will
be dependant on the pipe size, inner roughness of the pipe, flow velocity and
fluid viscosity. The flow condition, whether ‘Turbulent’ or not, will
determine the method used to calculate the friction factor. The starting point
must be to find the fluid’s viscosity. This will be the factor that has
most effect on the pipework losses.
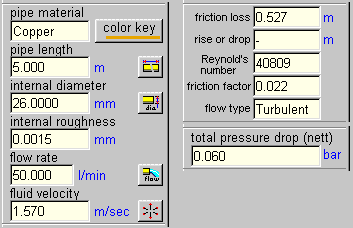
Understanding viscosity units (dynamic viscosity)
Many terms can be used to describe a fluid's viscosity (its resistance
to flow): Centipoise, Poise, Saybolt Universal (SSU), Saybolt Furol, Ford Cup
No. 3, Ford Cup No.4, Redwood No.1, Degrees Engler, Zahn No.1, Zahn No.2 and
Zahn No. 3 are some of the scales that have been used in the immediate past.
All of these scales have differing upper and lower values and are
usually not directly related to each other. Some references may be found in
text books which attempt to list equivalent values for these different methods
of measuring viscosity.
Pipe Flow 3D provides a means of calculating
the equivalent centistokes viscosity from some other known viscosity scales.
Kinematic viscosity and Reynold’s numbers
Dynamic
viscosity must be converted to its Kinematic viscosity equivalent before the
viscosity value can be used to calculate Reynold’s numbers and hence
friction factors.
It is very common today to express dynamic viscosity
in centipoise.
one Centipoise = 1 mPa.s or 0.001 (kg/m) x s
| The units of centipoise
are: |
Force per unit area x Time
|
|
It is very common today to express kinematic viscosity in
centistokes.
one Centistoke = 1 mm²/s or 0.000001 m²/s
| The units of
centistokes are: |
Length²
Time |
|
| Kinematic viscosity is
simply: |
Dynamic viscosity
Mass density |
|
Reynold’s numbers
Reynold’s
numbers (Re) describe the relationship between a fluid’s velocity, the
pipe size and the fluid’s kinematic viscosity.
| Reynold’s number
= |
Fluid velocity x
Internal pipe diameter
Kinematic viscosity |
|
Effect of the inner roughness of the pipe
The inner roughness of the pipe can create eddy currents. This
increases the friction between the pipe wall and the fluid. The relative
roughness of the inside of the pipe is used in determining the friction factor
to be used.
| Relative roughness =
|
Inside pipe roughness
Inside pipe diameter |
|
The average inner roughness of commercial
pipes:
Steel tube
Copper
tubing
Glass tubing
Polythene
Flexible P.V.C.
Rigid P.V.C.
Cast iron tube
Concrete tube
|
0.0460 mm
0.0015 mm
0.0001 mm
0.0010 mm
0.2000 mm
0.0050 mm
0.2600 mm
2.0000
mm
|
|
Friction factor chart
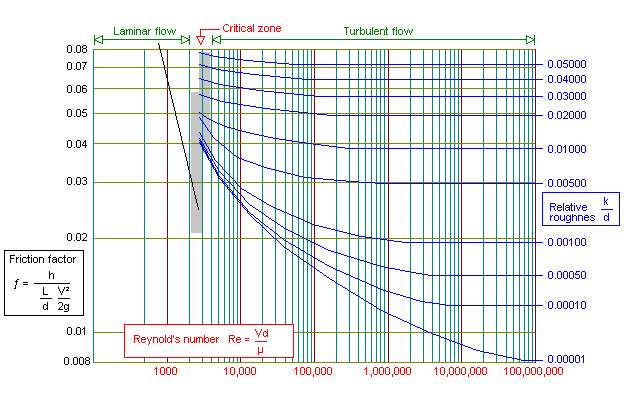
The chart above shows the relationship between
Reynold’s number and pipe friction.
Calculation of friction factors is
dependant on the type of flow that will be encountered.
For Re numbers
<2300 the fluid flow is Laminar, when Re number is >2300 the fluid flow
is Turbulent.
Laminar flow (Re < 2300) f = 64/Re
Turbulent flow
(Re > 2300) 1/sqrt(f) = -1.8 log [ (6.9/Re) + ((k/3.7)^1.11 ]
(where k =
inner pipe roughness / inner pipe diameter)
Most commercial
applications involve Turbulent flow. In these cases the inner roughness of the
pipework can have a significant effect on the Friction factor.
The
Relative roughness is the inner roughness divided by the internal diameter of
the pipe work.
The Friction factor is found by plotting the intersection of
Re and Relative roughness, and reading the friction factor on the left hand
axis of the chart.
The Fluid head loss can be calculated once the
friction factor is known.
The Pressure drop in pipe work can be calculated
from fluid head loss, the density of fluid and the acceleration due to
gravity.
Calculating the fluid head resistance
Fluid
head resistance can be calculated from h = f (L/d) x (v ²/2g)
where
h = head loss (m)
f = friction factor
L = length of
pipe work (m)
d = inner dia of pipe work (m)
v = velocity of fluid
(m/s)
g = acceleration due to gravity (m/s
²)
Calculating the losses through pipe work
fittings
The fluid head resistance through various pipe work
fittings can be calculated when the 'K' factor of the fitting is known.
Manufacturers of pipe work fittings & valves publish 'K' factors for their
products.
Usually a particular type of fitting from various
manufacturers have similar 'K' factors, therefore this computer program tends
to use average 'K' factor values.
Fluid head loss of these fitting can
be calculated from h = total 'K' x v ² / 2g
where
h = head
loss (m)
total 'K' = total of 'K' factors for each fitting
v = velocity
of fluid (m/s)
g = acceleration due to gravity (m/s ²)
Note: If
the pipework involves different pipe sizes, this calculation must be carried
out separately for each pipe size, using the appropriate velocity within that
pipe section.
The 'K' value of entry & exit points can be taken as
0.8 and 1.0 respectively to calculate the head loss attributable to these
features.
Calculating the total pressure drop
The
total fluid head resistance may be used to calculate the pressure required to
overcome the resistance to fluid flow.
Pd = h x p x g /
100000
where
Pd = pressure drop (bar)
h = head loss (m)
p
= fluid density (kg/m3)
g = acceleration due to gravity (m/s
²)
Finally, the fluid is most likely to exit into atmospheric
pressure. The difference between the pressure on the fluid surface during
storage & the atmospheric pressure must be taken into account in
determining the pressure drop to be overcome by the pump.
This
difference in pressure may be positive (assisting fluid flow) or negative
(resisting fluid flow).
Summarising the steps to be considered
Factors that affect fluid flow
Fluid flow in
pipes is affected by many different factors:
- The viscosity, density, and velocity of the fluid.
- Changes in the fluid temperature will change the viscosity
& density of the fluid.
- The length, inner diameter, and in the case of turbulent flow,
the internal roughness of the pipe.
- The position of the supply and discharge containers relative to
the pump position.
- The addition of rises & falls within the pipe layout.
- The number & types of bends in the pipe layout.
- The number & types of valves, & other fittings, in the
pipe layout.
- Entrance & exit conditions of the pipe work.
Calculating the fluid head
When all of the
above information is known, the following steps must be carried out to
determine the fluid head necessary to overcome the flow of the fluid through
the pipe work layout:
- Calculate the Reynolds number
- Determine if the flow is Laminar or Turbulent
- Calculate the friction factor for either Laminar flow or
Turbulent flow
- Calculate the fluid head resistance to overcome the flow
through the pipe work
- Determine the ‘K’ factors for the fittings within the
pipe work layout
- Calculate the fluid head resistance to overcome the flow
through the fittings
- Determine which lengths & components within the pipe work
layout are significant in establishing the maximum fluid head to be considered
(branch lines may be important).
The effect of fluid density & gravity must be applied to the
maximum fluid head to calculate the pressure required to overcome the
resistance to fluid flow.
|
Use Pipe Flow 3D to carry out your
calculations
Download PipeFlow 3D for a
FREE trial!
|
|
|